Rules of simplification
If a Boolean expression can be simplified and still produce the same output for a given set of inputs, this means that the corresponding combination of logic gates can also be simplified. Less logic gates in a circuit means less electronic components, which in turn makes circuits cheaper to produce, more efficient and more reliable. There are some rules that can be applied in order to simplify Boolean expressions. These are described below.
Av0 = A
Given that the OR operation is equivalent to addition, then this reads as A+0=A. If A is 1, then 1+0=1 and if A is 0, then 0+0=0, so the expression holds true. Indeed, this is the behaviour expected of an OR gate.
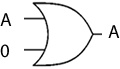
Av1 = 1
This reads as A+1=1. If A is 1, then 1+1=1 (there is only 1 or 0) and if A is 0, then 0+1=1, so the expression holds true. Once again, this is the behaviour expected of an OR gate.
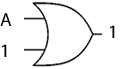
AvA = A
This reads as A+A=A. If A is 1, then 1+1=1 (there is only 1 or 0) and if A is 0, then 0+0=0, so the expression holds true. Once again, this is the behaviour expected of an OR gate.
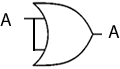
0^A = 0
Given that the AND operation is equivalent to multiplication, then this reads as 0*A=0. If A is 1, then 0*1=0 and if A is 0, then 0*0=0, so the expression holds true. Indeed, this is the behaviour expected of an AND gate.
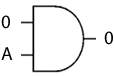
1^A = A
This reads as 1*A=A. If A is 1, then 1*1=1 and if A is 0, then 1*0=0, so the expression holds true. Once again, this is the behaviour expected of an AND gate.
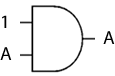
A^A = A
This reads as A*A=A. If A is 1, then 1*1=1 and if A is 0, then 0*0=0, so the expression holds true. Once again, this is the behaviour expected of an AND gate.
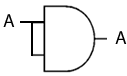
¬(¬A) = A
NOT NOT A = A. This should make perfect sense. The opposite of 1 is 0, and the opposite of the opposite of 1 is 1. Similarly, the opposite of 0 is 1, and the opposite of the opposite of 0 is 0. This can be seen with a pair of NOT gates. The first NOT gate inverts its input, and if this is inverted again we end up with what we started with.
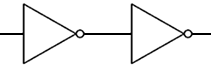
A v¬A = 1
A OR NOT A = 1. To explain this, first notice that if A is 1 then ¬A is 0, and if A is 0 then ¬A is 1. Hence either A or ¬A will always be 1 (they cannot be the same), so the calcualtion A plus ¬A is always going to yeild 1. Given that the OR operation is equivelent to addition, the expression A?¬A will always equate to 1. This rule can also be seen by examining the combination of gates that corresponds to this expression. Whatever the value of A, the output will always be 1.
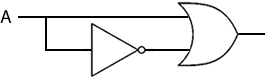
A ^¬A = 0
A AND NOT A = 0. Given that either A or ¬A will always be 0, and that the AND operation is equivelent to multiplication, the calcualtion A multiplied by ¬A is always going to yeild 0, so the expression A?¬A will always equate to 0. This rule can also be seen by examining the combination of gates that corresponds to this expression. Whatever the value of A, the output will always be zero.
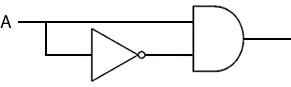
Laws of Boolean algebra
Number properties review
There are three basic properties of numbers, associative, commutative and distributive. These are particularly relevant to students of advanced mathematics, but you have probably already being applying them to denary arithmetic without a second thought.
You know that 5+(2+3)=10, and that this is the same as saying (5+2)+3=10. This illustrates something about the way these numbers can be grouped, specifically their associative property. The associative property can be expressed algebraically as: a+(b+c) = (a+b)+c. You no doubt also know that 5*(2*3)=30 and that (5*2)*3=30, hence we can say a(bc) = (ab)c.
The commutative property refers to the way numbers can be moved around in an expression, for example a+b = b+a. Similarly, ab = ba.
Finally, you may have solved problems that require you to ‘expand the brackets’ or, conversely, to factorise an expression. This relies on the distributive property, namely that a(b+c) = ab+ac. For example, 2*(3+4) = 2*3+2*4.
When it comes to Boolean algebra, there are some similar rules.
| Associative | (AvB)vC = Av(BvC) (A^B)^C = A^(B^C) |
| Commutative | AvB = BvA A^B = B^A |
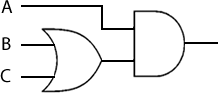
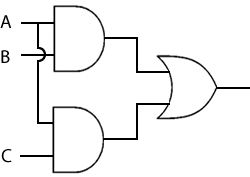
| Distributive | A^(BvC) = (A^B)v(A^C) Av(B^C) = (AvB)^(AvC) |
Look at the first expression of the distributive property in the table above. When the corresponding, equivalent, logic gate combinations are compared, it is immediately apparent that one requires fewer electronic components than the other.
| A^(BvC) | (A^B)v(A^C) | |
 |
 |
Download a presentation of the laws of Boolean algebra here
